Espandi la funzione in potenze x x0. Espansione di funzioni in serie di potenze

Nella teoria delle serie funzionali il posto centrale è occupato dalla sezione dedicata allo sviluppo di una funzione in una serie.

Pertanto, il compito è impostato: per una determinata funzione dobbiamo trovare una tale serie di potenze

che convergeva su un certo intervallo e la sua somma era uguale a
, quelli.

= ..

Questo compito si chiama il problema di espandere una funzione in una serie di potenze.

Condizione necessaria per la scomponibilità di una funzione in una serie di potenzeè la sua differenziabilità un numero infinito di volte - ciò deriva dalle proprietà delle serie di potenze convergenti. Questa condizione è soddisfatta, di regola, per le funzioni elementari nel loro dominio di definizione.

Quindi supponiamo che la funzione
ha derivate di qualsiasi ordine. È possibile espanderla in una serie di potenze? Se sì, come possiamo trovare questa serie? La seconda parte del problema è più semplice da risolvere, quindi cominciamo con essa.

Supponiamo che la funzione
può essere rappresentato come la somma di una serie di potenze convergenti nell'intervallo contenente il punto X 0 :

= .. (*)

Dove UN 0 ,UN 1 ,UN 2 ,...,UN P ,... – coefficienti sconosciuti (ancora).

Poniamo in uguaglianza (*) il valore x = x 0 , allora otteniamo

.

Differenziamo le serie di potenze (*) termine per termine

= ..

e credere qui x = x 0 , noi abbiamo

.

Con la differenziazione successiva otteniamo la serie

= ..

credendo x = x 0 , noi abbiamo
, Dove
.

Dopo P-differenziazione multipla che otteniamo

Supponendo nell'ultima uguaglianza x = x 0 , noi abbiamo
, Dove

Quindi, si trovano i coefficienti

,
,
, …,
,….,

sostituendo quale nella serie (*), otteniamo

La serie risultante viene chiamata accanto a Taylor per funzione
.

Pertanto, lo abbiamo stabilito se la funzione può essere sviluppata in una serie di potenze in potenze (x - x 0 ), allora questo sviluppo è unico e la serie risultante è necessariamente una serie di Taylor.

Si noti che la serie di Taylor può essere ottenuta per qualsiasi funzione che abbia derivate di qualsiasi ordine nel punto x = x 0 . Ma questo non significa che si possa mettere un segno uguale tra la funzione e la serie risultante, cioè che la somma della serie è uguale alla funzione originale. In primo luogo, tale uguaglianza può avere senso solo nella regione di convergenza e la serie di Taylor ottenuta per la funzione potrebbe divergere e, in secondo luogo, se la serie di Taylor converge, la sua somma potrebbe non coincidere con la funzione originale.

3.2. Condizioni sufficienti per la scomponibilità di una funzione in una serie di Taylor

Formuliamo una dichiarazione con l'aiuto della quale il compito sarà risolto.

Se la funzione
in qualche intorno del punto x 0 ha derivate fino a (N+ 1) di ordine compreso, quindi in questo quartiere abbiamoformula Taylor

DoveR N (X)-il termine resto della formula di Taylor – ha la forma (forma di Lagrange)

Dove puntoξ si trova tra x e x 0 .

Nota che c'è una differenza tra la serie di Taylor e la formula di Taylor: la formula di Taylor è una somma finita, cioè P - numero fisso.

Ricordiamo che la somma della serie S(X) può essere definito come il limite di una sequenza funzionale di somme parziali S P (X) ad un certo intervallo X:

.

Secondo questo, espandere una funzione in una serie di Taylor significa trovare una serie tale che per any XX

Scriviamo la formula di Taylor nella forma dove

notare che
definisce l'errore che otteniamo, sostituisce la funzione F(X) polinomio S N (X).

Se
, Quello
,quelli. la funzione viene espansa in una serie di Taylor. Viceversa, se
, Quello
.

Così abbiamo dimostrato criterio per la scomponibilità di una funzione in una serie di Taylor.

Affinché la funzioneF(x) si espande in una serie di Taylor, è necessario e sufficiente che su questo intervallo
, DoveR N (X) è il termine resto della serie di Taylor.

Utilizzando il criterio formulato si può ottenere sufficientecondizioni per la scomponibilità di una funzione in una serie di Taylor.

Se dentroqualche intorno del punto x 0 i valori assoluti di tutte le derivate della funzione sono limitati allo stesso numero M≥ 0, cioè

, To in questo intorno la funzione si espande in una serie di Taylor.

Da quanto sopra segue algoritmoespansione delle funzioni F(X) nella serie di Taylor in prossimità di un punto X 0 :

1. Trovare le derivate di funzioni F(X):

f(x), f’(x), f”(x), f’”(x), f (N) (X),…

2. Calcola il valore della funzione e i valori delle sue derivate nel punto X 0

f(x 0 ), f’(x 0 ), f”(x 0 ), f’”(x 0 ), F (N) (X 0 ),…

3. Scriviamo formalmente la serie di Taylor e troviamo la regione di convergenza della serie di potenze risultante.

4. Controlliamo l'adempimento di condizioni sufficienti, ad es. stabiliamo per quale X dalla regione di convergenza, termine residuo R N (X) tende a zero come
O
.

Viene chiamata l'espansione delle funzioni in una serie di Taylor utilizzando questo algoritmo espansione di una funzione in una serie di Taylor per definizione O decomposizione diretta.

"Trova lo sviluppo in serie di Maclaurin della funzione f(x)"- questo è esattamente come suona il compito di matematica superiore, cosa che alcuni studenti possono fare, mentre altri non riescono a far fronte agli esempi. Esistono diversi modi per espandere una serie in potenze; ​​qui forniremo una tecnica per espandere le funzioni in una serie di Maclaurin. Quando si sviluppa una funzione in una serie, è necessario essere bravi a calcolare le derivate.

Esempio 4.7 Espandi una funzione in potenze di x

Calcoli: Eseguiamo lo sviluppo della funzione secondo la formula di Maclaurin. Innanzitutto, espandiamo il denominatore della funzione in una serie

Infine, moltiplica l'espansione per il numeratore.
Il primo termine è il valore della funzione a zero f (0) = 1/3.
Troviamo le derivate della funzione del primo e dell'ordine superiore f (x) e il valore di queste derivate nel punto x=0




Successivamente, in base allo schema delle variazioni del valore dei derivati ​​a 0, scriviamo la formula per l'ennesimo derivato

Quindi, rappresentiamo il denominatore sotto forma di espansione nella serie Maclaurin

Moltiplichiamo per il numeratore e otteniamo l'espansione desiderata della funzione in una serie in potenze di x

Come puoi vedere, qui non c'è nulla di complicato.
Tutti i punti chiave si basano sulla capacità di calcolare le derivate e di generalizzare rapidamente il valore della derivata di ordine superiore pari a zero. I seguenti esempi ti aiuteranno a imparare come organizzare rapidamente una funzione in una serie.

Esempio 4.10 Trovare lo sviluppo in serie di Maclaurin della funzione

Calcoli: come avrai intuito, inseriremo il coseno al numeratore di una serie. Per fare ciò, puoi utilizzare formule per quantità infinitesimali, oppure ricavare lo sviluppo del coseno tramite le derivate. Di conseguenza, arriviamo alla seguente serie in potenze di x

Come puoi vedere, abbiamo un minimo di calcoli e una rappresentazione compatta dell'espansione in serie.

Esempio 4.16 Espandi una funzione in potenze di x:
7/(12-x-x^2)
Calcoli: In questo tipo di esempi è necessario espandere la frazione tramite la somma di frazioni semplici.
Non mostreremo ora come farlo, ma con l'aiuto di coefficienti indefiniti arriveremo alla somma delle frazioni.
Successivamente scriviamo i denominatori in forma esponenziale

Resta da espandere i termini utilizzando la formula di Maclaurin. Sommando i termini alle stesse potenze di “x”, componiamo una formula per il termine generale dello sviluppo di una funzione in una serie



L'ultima parte del passaggio alla serie all'inizio è difficile da implementare, poiché è difficile combinare le formule per gli indici (gradi) accoppiati e non accoppiati, ma con la pratica migliorerai.

Esempio 4.18 Trovare lo sviluppo in serie di Maclaurin della funzione

Calcoli: Troviamo la derivata di questa funzione:

Espandiamo la funzione in una serie utilizzando una delle formule di McLaren:

Sommiamo le serie termine per termine in base al fatto che entrambe sono assolutamente identiche. Avendo integrato l'intera serie termine per termine, otteniamo lo sviluppo della funzione in una serie in potenze di x

C'è una transizione tra le ultime due righe dell'espansione che all'inizio richiederà molto tempo. Generalizzare una formula in serie non è facile per tutti, quindi non preoccuparti di non riuscire a ottenere una formula bella e compatta.

Esempio 4.28 Trovare lo sviluppo in serie di Maclaurin della funzione:

Scriviamo il logaritmo come segue

Usando la formula di Maclaurin, espandiamo la funzione logaritmo in una serie in potenze di x

La convoluzione finale è complessa a prima vista, ma alternando i segni otterrai sempre qualcosa di simile. La lezione di input sull'argomento delle funzioni di pianificazione in fila è completata. Altri schemi di scomposizione altrettanto interessanti saranno discussi in dettaglio nei seguenti materiali.

Se la funzione f(x) ha un intervallo contenente il punto UN, derivate di tutti gli ordini, allora ad essa può essere applicata la formula di Taylor:

Dove r n– il cosiddetto termine resto o resto della serie, può essere stimato utilizzando la formula di Lagrange:

, dove il numero x è compreso tra X E UN.

Se per qualche valore xr n®0 a N®¥, allora nel limite la formula di Taylor diventa una formula convergente per questo valore Serie di Taylor:

Quindi la funzione f(x) può essere espanso in una serie di Taylor nel punto in questione X, Se:

1) ha derivati ​​di tutti gli ordini;

2) la serie costruita converge in questo punto.

A UN=0 otteniamo una serie chiamata vicino a Maclaurin:

Esempio 1 f(x)= 2X.

Soluzione. Troviamo i valori della funzione e delle sue derivate a X=0

f(x) = 2X, F( 0) = 2 0 =1;

f¢(x) = 2X ln2, f¢( 0) = 2 0 ln2=ln2;

f¢¢(x) = 2X ln 2 2, f¢¢( 0) = 2 0 ln22=ln222;

f(n)(x) = 2X ln N 2, f(n)( 0) = 2 0 ln N 2=ln N 2.

Sostituendo i valori ottenuti delle derivate nella formula della serie di Taylor, otteniamo:

Il raggio di convergenza di questa serie è uguale a infinito, quindi questa espansione vale per -¥<X<+¥.

Esempio 2 X+4) per la funzione f(x)= e X.

Soluzione. Trovare le derivate della funzione e X e i loro valori al punto X=-4.

f(x)= e X, F(-4) = e -4 ;

f¢(x)= e X, f¢(-4) = e -4 ;

f¢¢(x)= e X, f¢¢(-4) = e -4 ;

f(n)(x)= e X, f(n)( -4) = e -4 .

Pertanto, la serie di Taylor richiesta della funzione ha la forma:

Questa espansione è valida anche per -¥<X<+¥.

Esempio 3 . Espandi una funzione f(x)= ln X in una serie di potenze ( X- 1),

(cioè nella serie di Taylor in prossimità del punto X=1).

Soluzione. Trova le derivate di questa funzione.

Sostituendo questi valori nella formula, otteniamo la serie di Taylor desiderata:

Usando il test di d'Alembert, puoi verificare che la serie converge quando

½ X- 1½<1. Действительно,

La serie converge se ½ X- 1½<1, т.е. при 0<X<2. При X=2 otteniamo una serie alternata che soddisfa le condizioni del criterio di Leibniz. A X=0 la funzione non è definita. Pertanto, la regione di convergenza della serie di Taylor è l'intervallo semiaperto (0;2].

Presentiamo gli sviluppi così ottenuti nella serie di Maclaurin (cioè in prossimità del punto X=0) per alcune funzioni elementari:

(2) ,

(3) ,

( viene chiamata l'ultima scomposizione serie binomiale)

Esempio 4 . Espandi la funzione in una serie di potenze

Soluzione. Nell'espansione (1) sostituiamo X SU - X 2, otteniamo:

Esempio 5 . Espandi la funzione in una serie Maclaurin

Soluzione. Abbiamo

Usando la formula (4), possiamo scrivere:

sostituendo invece X nella formula -X, noi abbiamo:

Da qui troviamo:

Aprendo le parentesi, riordinando i termini della serie e riportando termini simili, otteniamo

Questa serie converge nell'intervallo

(-1;1), poiché è ottenuto da due serie, ciascuna delle quali converge in questo intervallo.

Commento .

Le formule (1)-(5) possono essere utilizzate anche per espandere le funzioni corrispondenti in una serie di Taylor, ovvero per espandere funzioni in potenze intere positive ( Ah). Per fare ciò è necessario eseguire tali identiche trasformazioni su una data funzione in modo da ottenere una delle funzioni (1)-(5), in cui invece X costi k( Ah) m , dove k è un numero costante, m è un numero intero positivo. Spesso conviene effettuare un cambio di variabile T=Ah ed espandere la funzione risultante rispetto a t nella serie di Maclaurin.

Questo metodo illustra il teorema sull'unicità dello sviluppo di una funzione in serie di potenze. L'essenza di questo teorema è che nell'intorno di uno stesso punto non si possono ottenere due serie di potenze diverse che convergano alla stessa funzione, qualunque sia il modo in cui viene eseguita la sua espansione.

Esempio 6 . Espandi la funzione in una serie di Taylor in un intorno di un punto X=3.

Soluzione. Questo problema può essere risolto, come prima, utilizzando la definizione della serie di Taylor, per la quale dobbiamo trovare le derivate della funzione e i loro valori in X=3. Tuttavia, sarà più semplice utilizzare l'espansione esistente (5):

La serie risultante converge a o –3<X- 3<3, 0<X< 6 и является искомым рядом Тейлора для данной функции.

Esempio 7 . Scrivi la serie di Taylor in potenze ( X-1) funzioni .

Soluzione.

La serie converge a , o 2< X£ 5.

Tra le serie funzionali il posto più importante è occupato dalle serie di potenze.

Una serie di potenze è una serie

i cui termini sono funzioni di potenza disposte in potenze intere crescenti non negative X, UN C0 , C 1 , C 2 , C N - valori costanti. Numeri C1 , C 2 , C N - coefficienti dei termini della serie, C0 - membro gratuito. I termini della serie di potenze sono definiti sull'intera retta numerica.

Facciamo conoscenza con il concetto Aree di convergenza delle serie di potenze. Questo è un insieme di valori variabili X, per cui la serie converge. Le serie di potenze hanno una regione di convergenza abbastanza semplice. Per valori variabili reali X la regione di convergenza è costituita da un punto, oppure è un certo intervallo (intervallo di convergenza), oppure coincide con l'intero asse Bue .

Quando si sostituiscono i valori nella serie di potenze X= 0 risulterà in una serie numerica

C0 +0+0+...+0+... ,

che converge.

Pertanto, quando X= 0 qualsiasi serie di potenze converge e, quindi, la sua area di convergenza non può essere l'insieme vuoto. La struttura della regione di convergenza di tutte le serie di potenze è la stessa. Può essere stabilito utilizzando il seguente teorema.

Teorema 1 (teorema di Abele). Se una serie di potenze converge a un certo valore X = X 0 , diverso da zero, allora converge, e peraltro in assoluto, per tutti i valori |X| < |X 0 | . Nota: sia il valore iniziale "X è zero" sia qualsiasi valore di "X" confrontato con il valore iniziale vengono presi modulo - senza tenere conto del segno.

Conseguenza. Se la serie di potenze diverge ad un certo valore X = X 1 , allora diverge per tutti i valori |X| > |X 1 | .

Come abbiamo già scoperto in precedenza, qualsiasi serie di potenze converge al valore X= 0. Esistono serie di potenze che convergono solo quando X= 0 e divergono per altri valori X. Escludendo questo caso dalla considerazione, assumiamo che la serie di potenze converga ad un certo valore X = X 0 , diverso da zero. Allora, secondo il teorema di Abel, converge in tutti i punti dell'intervallo ]-| X0 |, |X 0 |[ (intervallo i cui confini sinistro e destro sono i valori x a cui converge la serie di potenze, presi rispettivamente con un segno meno e un segno più), simmetrico rispetto all'origine.

Se la serie di potenze diverge per un certo valore X = X 1 , allora, in base ad un corollario del teorema di Abel, diverge in tutti i punti esterni al segmento [-| X1 |, |X 1 |] . Ne consegue che per ogni serie di potenze esiste un intervallo simmetrico rispetto all'origine, detto intervallo di convergenza , in ogni punto in cui la serie converge, ai bordi può convergere, oppure può divergere, e non necessariamente contemporaneamente, e all'esterno del segmento la serie diverge. Numero Rè detto raggio di convergenza della serie di potenze.

In casi speciali intervallo di convergenza delle serie di potenze può degenerare fino a un punto (allora la serie converge solo quando X= 0 e si considera tale R= 0) oppure rappresentare l'intera retta numerica (quindi la serie converge in tutti i punti della retta numerica e si assume che ).

Pertanto, determinare la regione di convergenza di una serie di potenze consiste nel determinarne la regione raggio di convergenza R e studiare la convergenza delle serie ai confini dell'intervallo di convergenza (a ).

Teorema 2. Se tutti i coefficienti di una serie di potenze, a partire da uno, sono diversi da zero, allora il suo raggio di convergenza è uguale al limite pari al rapporto tra i valori assoluti dei coefficienti dei seguenti membri comuni della serie , cioè.

Esempio 1. Trova la regione di convergenza della serie di potenze

Soluzione. Qui

Utilizzando la formula (28), troviamo il raggio di convergenza di questa serie:

Studiamo la convergenza della serie agli estremi dell'intervallo di convergenza. L'esempio 13 mostra che questa serie converge a X= 1 e diverge in X= -1. Di conseguenza, la regione di convergenza è il semiintervallo.

Esempio 2. Trova la regione di convergenza della serie di potenze

Soluzione. I coefficienti della serie sono positivi e

Troviamo il limite di questo rapporto, cioè raggio di convergenza della serie di potenze:

Studiamo la convergenza della serie agli estremi dell'intervallo. Sostituzione di valori X= -1/5 e X= 1/5 in questa riga dà:

La prima di queste serie converge (vedi Esempio 5). Ma allora, in virtù del teorema della sezione “Convergenza assoluta”, anche la seconda serie converge, e la regione della sua convergenza è il segmento

Esempio 3. Trova la regione di convergenza della serie di potenze

Soluzione. Qui

Utilizzando la formula (28) troviamo il raggio di convergenza della serie:

Studiamo la convergenza della serie per valori di . Sostituendoli in questa serie, otteniamo rispettivamente

Entrambe le serie divergono perché la condizione necessaria per la convergenza non è soddisfatta (i loro termini comuni non tendono a zero in ). Quindi, ad entrambe le estremità dell'intervallo di convergenza, questa serie diverge e la regione della sua convergenza è l'intervallo.

Esempio 5. Trova la regione di convergenza della serie di potenze

Soluzione. Troviamo la relazione dove , e :

Secondo la formula (28), il raggio di convergenza di questa serie

,

cioè la serie converge solo quando X= 0 e diverge per altri valori X.

Gli esempi mostrano che alle estremità dell'intervallo di convergenza le serie si comportano diversamente. Nell'esempio 1, ad un'estremità dell'intervallo di convergenza la serie converge e all'altra diverge; nell'esempio 2 converge ad entrambe le estremità; nell'esempio 3 diverge ad entrambe le estremità.

La formula per il raggio di convergenza di una serie di potenze si ottiene assumendo che tutti i coefficienti dei termini della serie, a partire da un certo punto, siano diversi da zero. Pertanto, l'uso della formula (28) è consentito solo in questi casi. Se questa condizione viene violata, è necessario cercare il raggio di convergenza della serie di potenze Segno di d'Alembert, oppure, sostituendo la variabile, trasformando la serie in una forma in cui la condizione specificata è soddisfatta.

Esempio 6. Trova l'intervallo di convergenza della serie di potenze

Soluzione. Questa serie non contiene termini con gradi dispari X. Trasformiamo quindi la serie, ponendo . Quindi otteniamo la serie

per trovare il raggio di convergenza del quale possiamo applicare la formula (28). Poiché , a , allora il raggio di convergenza di questa serie

Dall'uguaglianza che otteniamo, quindi, questa serie converge sull'intervallo .

Somma di serie di potenze. Differenziazione e integrazione di serie di potenze

Consideriamo la serie di potenze

raggio di convergenza R> 0, cioè questa serie converge sull'intervallo .

Quindi ogni valore X dall'intervallo di convergenza corrisponde ad una certa somma della serie. Pertanto la somma delle serie di potenze è funzione di X sull'intervallo di convergenza. Indicandolo con F(X), possiamo scrivere l'uguaglianza

intendendolo nel senso che la somma delle serie in ogni punto X dall'intervallo di convergenza è uguale al valore della funzione F(X) a questo punto. Nello stesso senso diremo che la serie di potenze (29) converge alla funzione F(X) sull'intervallo di convergenza.

Al di fuori dell’intervallo di convergenza l’uguaglianza (30) non ha senso.

Esempio 7. Trova la somma delle serie di potenze

Soluzione. Questa è una serie geometrica per la quale UN= 1, a Q= X. Pertanto la sua somma è una funzione . Una serie converge se , ed è il suo intervallo di convergenza. Quindi uguaglianza

è valido solo per i valori, sebbene la funzione definito per tutti i valori X, tranne X= 1.

Si può dimostrare che la somma delle serie di potenze F(X) è continua e differenziabile su qualsiasi intervallo all'interno dell'intervallo di convergenza, in particolare in qualsiasi punto dell'intervallo di convergenza della serie.

Presentiamo i teoremi sulla differenziazione termine per termine e sull'integrazione delle serie di potenze.

Teorema 1. La serie di potenze (30) nell'intervallo della sua convergenza può essere differenziata termine per termine un numero illimitato di volte, e le serie di potenze risultanti hanno lo stesso raggio di convergenza della serie originale, e le loro somme sono rispettivamente pari a .

Teorema 2. Le serie di potenze (30) possono essere integrate termine per termine un numero illimitato di volte nell'intervallo da 0 a X, se , e la serie di potenze risultante hanno lo stesso raggio di convergenza della serie originale e le loro somme sono corrispondentemente uguali

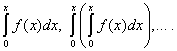
Espansione di funzioni in serie di potenze

Sia data la funzione F(X), che deve essere espanso in una serie di potenze, cioè rappresentare nella forma (30):

Il compito è determinare i coefficienti riga (30). Per fare ciò, differenziando l’uguaglianza (30) termine per termine, troviamo costantemente:

……………………………………………….. (31)

Assumendo nelle uguaglianze (30) e (31) X= 0, troviamo

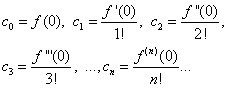
Sostituendo le espressioni trovate nell'uguaglianza (30), otteniamo

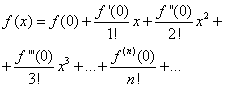(32)

Troviamo lo sviluppo in serie di Maclaurin di alcune funzioni elementari.

Esempio 8. Espandi la funzione in una serie Maclaurin

Soluzione. Le derivate di questa funzione coincidono con la funzione stessa:

Pertanto, quando X= 0 abbiamo

Sostituendo questi valori nella formula (32), otteniamo l'espansione desiderata:

(33)

Questa serie converge sull'intera linea numerica (il suo raggio di convergenza).

Gli studenti di matematica superiore dovrebbero sapere che la somma di una certa serie di potenze appartenente all'intervallo di convergenza della serie a noi data risulta essere una funzione continua e illimitata un numero di volte differenziata. Sorge la domanda: è possibile dire che una data funzione arbitraria f(x) è la somma di una certa serie di potenze? Cioè, a quali condizioni la funzione f(x) può essere rappresentata da una serie di potenze? L'importanza di questa domanda sta nel fatto che è possibile sostituire approssimativamente la funzione f(x) con la somma dei primi termini di una serie di potenze, cioè un polinomio. Questa sostituzione di una funzione con un'espressione piuttosto semplice - un polinomio - è utile anche quando si risolvono determinati problemi, vale a dire: quando si risolvono integrali, quando si calcola, ecc.

È stato dimostrato che per una certa funzione f(x), nella quale è possibile calcolare le derivate fino all’(n+1)esimo ordine, compreso l’ultimo, nell’intorno di (α - R; x 0 + R ) qualche punto x = α, è vero che la formula:

Questa formula prende il nome dalla famosa scienziata Brooke Taylor. La serie che si ottiene dalla precedente è detta serie di Maclaurin:

La regola che rende possibile eseguire un'espansione in una serie di Maclaurin:

1. Determinare le derivate del primo, secondo, terzo... ordine.
2. Calcola a quanto corrispondono le derivate in x=0.
3. Annota la serie di Maclaurin per questa funzione e quindi determina l'intervallo della sua convergenza.
4. Determina l'intervallo (-R;R), dove si trova il resto della formula di Maclaurin

R n (x) -> 0 in n -> infinito. Se ne esiste una, la funzione f(x) in essa contenuta deve coincidere con la somma della serie di Maclaurin.

Consideriamo ora la serie Maclaurin per le singole funzioni.

1. Quindi il primo sarà f(x) = e x. Naturalmente, per le sue caratteristiche, tale funzione ha derivate di ordine molto diverso, e f (k) (x) = e x , dove k è uguale a tutti. Sostituisci x = 0. Otteniamo f (k) (0) = e 0 =1, k = 1,2... In base a quanto sopra, la serie e x sarà simile a questa:

2. Serie di Maclaurin per la funzione f(x) = sin x. Chiariamo subito che la funzione per tutte le incognite avrà derivate, inoltre, f "(x) = cos x = sin(x+n/2), f "" (x) = -sin x = sin(x + 2*n/2)..., f (k) (x) = sin(x+k*n/2), dove k è uguale a un qualsiasi numero naturale, ovvero dopo aver fatto semplici calcoli possiamo arrivare a la conclusione che la serie per f(x) = sin x sarà simile a questa:

3. Proviamo ora a considerare la funzione f(x) = cos x. Per tutte le incognite ha derivate di ordine arbitrario, e |f (k) (x)| = |cos(x+k*n/2)|<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так:

Quindi, abbiamo elencato le funzioni più importanti che possono essere espanse in una serie di Maclaurin, ma per alcune funzioni sono integrate dalle serie di Taylor. Ora li elencheremo. Vale anche la pena notare che le serie di Taylor e Maclaurin costituiscono una parte importante del lavoro pratico sulla risoluzione delle serie in matematica superiore. Quindi, serie di Taylor.

1. La prima sarà la serie per la funzione f(x) = ln(1+x). Come negli esempi precedenti, per il dato f(x) = ln(1+x) possiamo sommare le serie utilizzando la forma generale della serie di Maclaurin. per questa funzione però è possibile ottenere la serie Maclaurin in modo molto più semplice. Avendo integrato una certa serie geometrica, otteniamo una serie per f(x) = ln(1+x) di tale campione:

2. E la seconda, che sarà l'ultima nel nostro articolo, sarà la serie per f(x) = arctan x. Per x appartenente all'intervallo [-1;1] vale l'espansione:

È tutto. Questo articolo ha esaminato le serie di Taylor e Maclaurin più utilizzate nella matematica superiore, in particolare nelle università economiche e tecniche.